강화학습_(r8)

1. 개요2. 원리3. 알고리즘

3.1. 가치 기반 알고리즘3.2. 정책 경사 알고리즘

1. 개요[편집]

強化學習 / Reinforcement learning

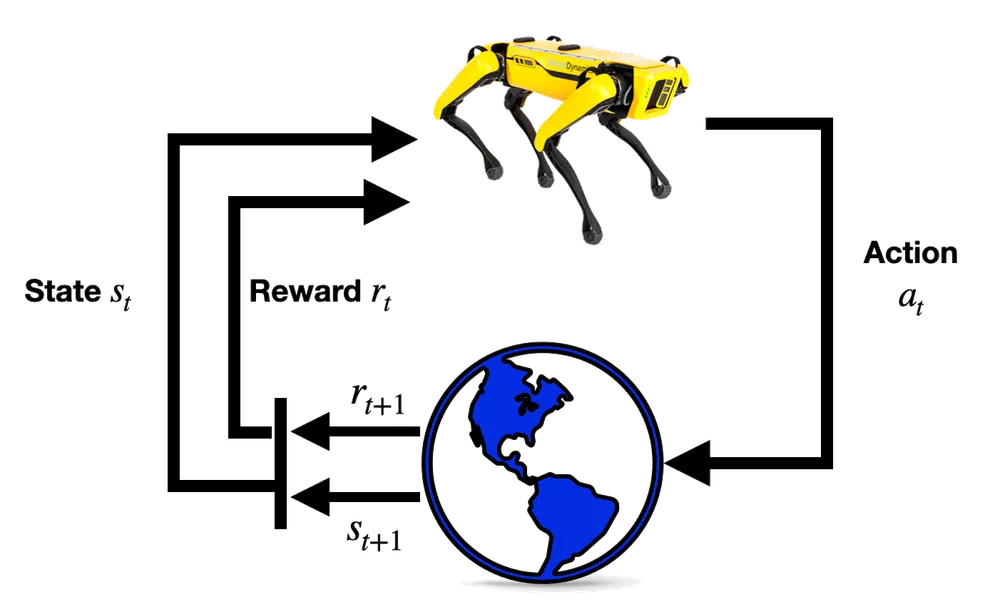
강화학습은 동물의 학습 능력을 모방한 것으로, 특정 상태(state)에서 어떤 행동(action)을 취하는 것이 최적인지를 학습하는 것이다.

강화학습의 주요한 기원 중 하나는 MDP(Markov Decision Process)가 있다. MDP는 1960년대 제안된 방법으로, 확률적 의사결정 문제를 수학적으로 정의하기 위한 프레임워크로 이해할 수 있다. 어떤 상태 S에서 행동 A를 취하면 보상 R을 받는 구조를 통해 심리학의 보상 기반 학습 개념을 수학적으로 모델링하였다.

강화학습의 또 다른 기원으로는 벨만 방정식이 있다. 1950년대, 동적 프로그래밍을 비롯한 제어이론을 연구하던 미국의 응용수학자 리처드 E. 벨만은 제어 문제를 재귀적인 형태[1]로 정의하였으며, 이를 벨만 방정식이라고 불렀다. 당시에는 연료, 에너지, 시간 등 다양한 요소로 정의된 비용을 최소화하는 방식으로 문제를 해결하였다. 이러한 비용 최소화 문제를 보상 최대화 문제로 등가 변환하는 관점을 채택하는데 이것이 강화학습으로 연결된다.

이 두 이론이 결합된 것이 바로 강화학습의 이론적 기초가 된다. 즉, 보상 기반의 확률적 의사결정 문제를 벨만 방정식을 이용하여 재귀적으로 해석하는 것이 강화학습 이론의 수학적 핵심이라 할 수 있다.

강화학습을 구성하는 주요한 구성요소는 다음과 같다.

에이전트(Agent): 강화학습 문제 상황에서 학습 혹은 행동의 주체가 되는 시스템을 말한다. 다음과 같은 하위 구성요소를 지닌다.
- 상태(State, $s$ ): 에이전트가 환경을 관찰한 결과
- 행동(Action, $a$ ): 환경을 관찰한 에이전트의 선택
- 정책(Policy, $pi(a|s)$ ): 상태에 따른 행동을 선택하는 전략
- 가치 함수(Value function): 정책하에서 미래 보상의 기댓값
  - 상태 가치 함수(State Value Function, $V^{pi}(s)$ ): 어떤 정책 $pi$ 를 따를 때, 상태 $s$ 가 가지는 미래 보상의 기댓값.
  - 행동 가치 함수(Action Value Function, $Q^{pi}(s, a)$ ): 어떤 정책 $pi$ 를 따를 때, 상태 $s$ 에서 행동 $a$ 를 선택할때 가지는 미래 보상의 기댓값
환경(environments): 에이전트가 상호작용하는 외부 세계를 의미하며, 다음과 같은 구성요소로 정의된다.
- 상태공간(State Space, $S$ ): 환경이 정의하는, Agent가 가질 수 있는 모든 상태의 집합
- 행동공간(Action Space, $A$ ): 환경이 정의하는, Agent가 선택할 수 있는 모든 행동의 집합
- 상태 전이 함수(State Transition Function, $P(s'|s, a)$ ): 에이전트가 상태 $s$ 에서 행동 $a$ 를 선택할 때, 다음 상태를 정의하는 함수
- 보상 함수(Reward Function, $R(s, a)$ ): 에이전트가 상태 $s$ 에서 행동 $a$ 를 선택할 때, 그 결과로 제공될 보상을 정의하는 함수
  - 보상(Reward, $r$ ): 보상함수의 결과값

3. 알고리즘[편집]

강화학습의 알고리즘은 가치 함수를 최적화 하는가? 아니면 정책 함수를 최적화하는가? 라는 기준에 따른 대분류를 가진다.

3.1. 가치 기반 알고리즘[편집]

소위 가치함수라고 불리는 Q함수, 행동 가치 함수를 최적화하는 알고리즘. 정책함수를 필요로 하는 on-policy 기법과 정책함수 없이 Q함수만 이용하는 전략인 off-poilcy 기법으로 나뉜다.

Q-learning
SARSA
DQN

3.2. 정책 경사 알고리즘[편집]

근본적인 에이전트의 행동원리인 정책함수를 요구로하는 알고리즘. 현재 가장 대세적인 방법이며, 사전학습된 인공신경망을 정책함수로 가정하여 적절한 리워드를 통해 입맛에 맞게 가공하는 기법이 유행중이다. 이 분야의 대표주자는 ChatGPT로 PPO와 RLHF[2]기법을 이용한 것으로 유명하다.

REINFORCE
A2C
TRPO
PPO

[1]

a_{n+1}=f(a_n)

의 형태로 소위 점화식이라 불리는 형태를 의미한다.[2] Reinforcement Learning from Human Feedback.